どうも。
"萌え命"
500mLです。
今日は数学ブログです。
導入
「メルカリ問題」とは、私が今日メルカリを見ていて思いついた問題です。
メルカリってご存知ですか?
↑これのことです。
それと、喜多郁代さんってご存知ですか?
↑かわいいね。
今日、私は喜多郁代さんのかわいいフィギュアをメルカリで見ておりました。
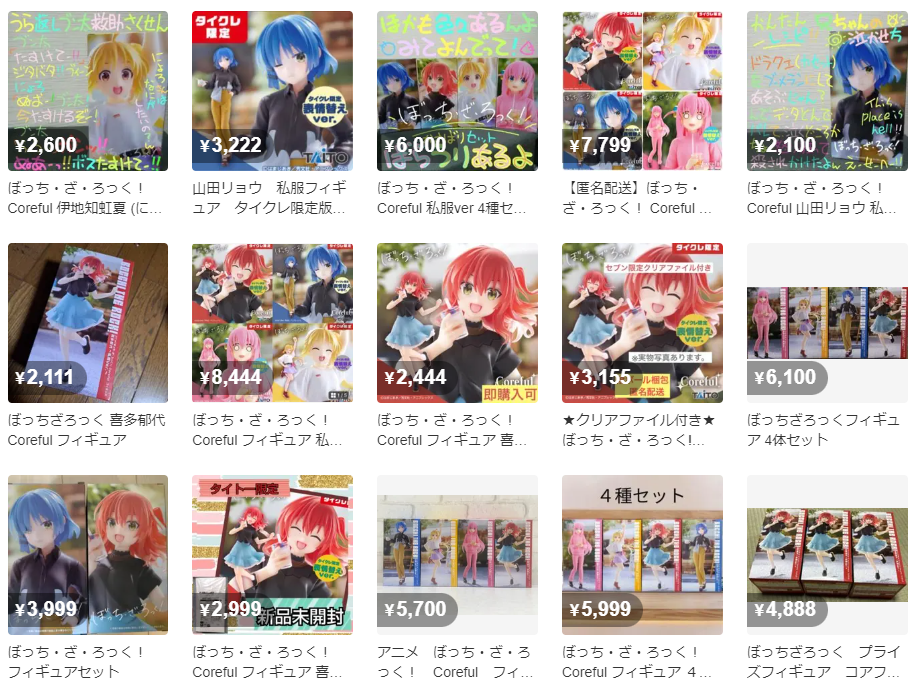
すると、ごらんのように、単品だけで喜多郁代さんのフィギュアを売っている人だけでなく、「セット販売」を行っている人がいるのです。
他のキャラとセットで売っている人もおりますが、右下に3つ同じフィギュアを売っている人も見えますね。いわゆる保存用・観賞用・布教用でしょうか。
そこで私は思うわけです。
「これ、喜多郁代さん一人分の相場は結局いくらなんだろう」
それを近似的に知るためには、価格をセットにされている数で割って平均をとればよさそうですが、めんどくさがりな私はこう思いました。
「価格だけを入力して、喜多郁代さん一人分の相場を計算できないだろうか」
これが、メルカリ問題です。この問題を数学的に定式化すると以下のようになります。
問題設定
ある商品の1つあたりの価格を、
とする。
あるフリマサイトでは、商品を販売している販売者が
人おり、
番目の販売者は商品
を
個まとめて販売している。そのときの価格は
円である。
ここで、データ列から、
を推定せよ。
解法
この問題は、離散フーリエ変換を用いれば解けます。
離散フーリエ変換とは
こんなんググれば出てくるんでざっくり解説します。
フーリエ変換とは、信号を時間領域から周波数領域で見るようにするための変換でした。
離散では、数列からその数列の繰り返し回数(位数とか言われますよね)を発見できます。(例えば、1, 2, 5, 1, 2, 5, ... みたいなのは位数3です)
↑この説明はあまりにも適当すぎます、もっと真面目に解説してほしいという人は信号処理の教科書とか読んでください。
こういう位数を発見するみたいなフーリエ変換といえば、Shorのアルゴリズムとかでも使われてますよね。
https://utokyo-icepp.github.io/qc-workbook/ja/shor.html
実際に解いてみた
pythonコードを書いて実行してみたのがこちら。

いい感じに解けてそう。
問題点
今回は変換する配列の番目の要素に、データ列
中に
が出現する回数を入れてます([1, 3, 5]なら[0, 1, 0, 1, 0, 1]みたいな)が、これってデータ次第では完全な周期関数になるとは限らないので厳密な解き方ではないです。
ちょっとをばらけさせても解けそうなことも確認はできてるんですが、
がある程度の確率分布に従うことを仮定してやりたいと思ったとき、
が大きいと
の分散が大きくなることが考えられるので、
が大きめのやつしかないデータからだと推定が難しくなりますよね。どうすればいいかなあ
なんかもっとスマートな方法ってないですか?あれば教えてください。
おわり
